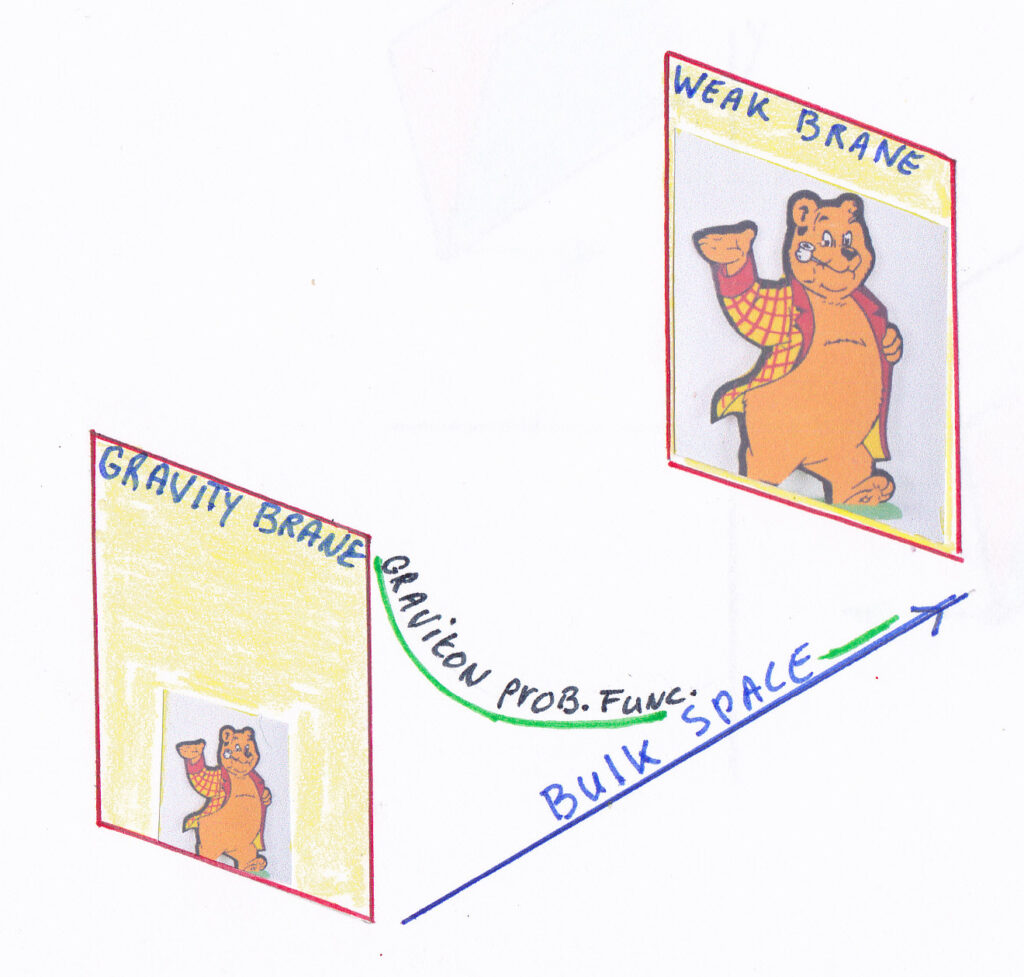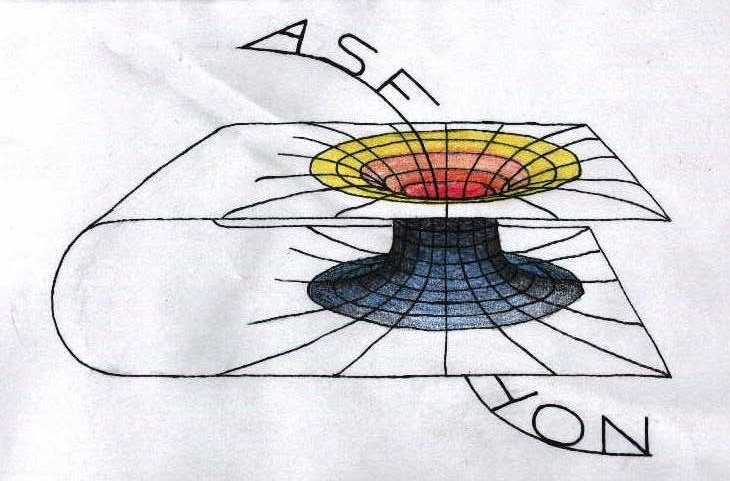

Asfyon was founded in 1994 by a group of a physicist as an independent research institute. For the members, there is a platform where they can present their research, projects, etc : www.asfyon.org (under construction)
contact: info@asfyon.com (reinoudjan@gmail.com)